If you believe what you read in the Daily Telegraph saving the planet must mean trashing the economy. That’s their story and they’re sticking to it, no matter what the evidence shows. If the numbers show the opposite, well, they have ways.
And so last week the Murdoch tabloid took a bunch of numbers concocted in Environment Minister Greg Hunt’s office and turned them into the screaming headline “ALP’s $600B Carbon Bill”.
One of the most egregious beat-ups you’ll ever read, the story was chock full of terrifying predictions about what will happen if Australia joins global efforts to limit global warming. The story was full of “shocking predictions”: “Economic growth shattered”, “Thousand of jobs lost”, and “a devastating blow to the economy, slashing thousands of jobs”.
The story was purportedly based on modelling results commissioned by the Climate Change Authority from Treasury and the then Department of Climate Change. Yet the conclusions Minister Hunt and the Telegraph reached were the opposite of those drawn by Treasury (and endorsed by the Climate Change Authority in its 2014 report).
Gazing at the same modelling printouts, Treasury wrote that the economic effects of all scenarios considered “are small compared with the ongoing growth in GDP and GNI per person over time” (p. 72).
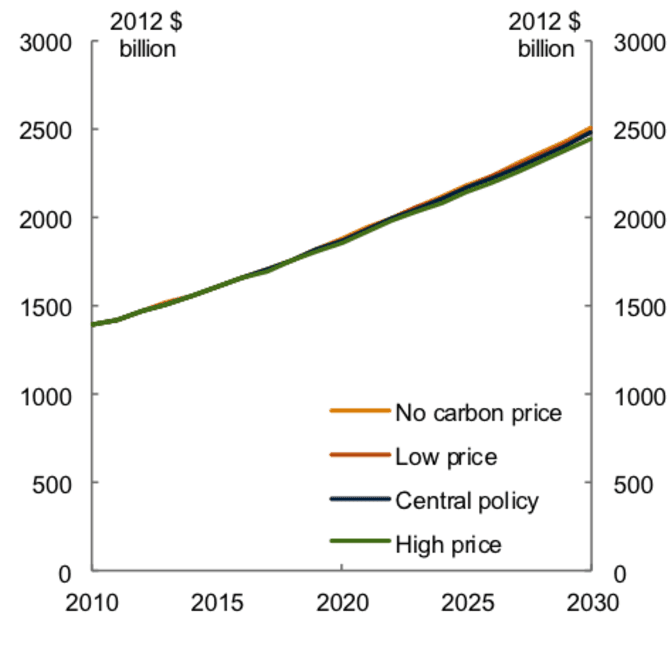
They present “only modestly different economic outlooks”, wrote the boffins. In fact, so modest are the economic effects of even strong climate action that when they are depicted on a chart it is quite difficult to pick out the difference between the “No carbon price” scenario and the “High price” scenario, the gap that the Telegraph, and Minister Hunt, claim would “shatter” the economy.
I reproduce Chart 3.32 from the Treasury report above, which measures real GDP over 2010-2030, the same figures that the Telegraph found “shocking”. You might need a magnifying glass to see it but all of the fuss is over the gap between the mustard coloured top line and the green bottom line. It is this difference that will wreck the Australian economy, if you believe Minister Hunt and his friends at the Telegraph.
To Do Nothing or Not To Do Nothing
It turns out that the Minister’s office possesses a very large magnifying glass indeed. But before they used it they needed to decide what to look at, and here they engaged in several blatant deceptions.
First they compared the “No carbon price” (do nothing) scenario with the “High price” scenario (limit warming to 2°C) and attributed the difference in economic trajectories to Labor’s planned policy. Apart from the fact that Labor has not adopted the latter policy (although in my view it should), this comparison is irrelevant.
No government is going to pursue the do-nothing “No carbon price” trajectory, which would mean abolishing the Direct Action scheme, the Renewable Energy Target and everything else.
The Abbott Government has itself just announced a target that is similar to the “Central policy” scenario (the blue line in the chart). Any policy to cut emissions will impose a cost, so the Government’s 26-28% by 2030 target will be a “hit” to real GDP that will account for a large chunk of the $600 billion.
Secondly, Treasury’s horrifying “High price” scenario is the only one that would limit global warming to 2°C. The 2°C objective is the official policy of the present Government, so by concocting these figures Minister Hunt is undermining himself (unless he is deceiving us over his commitment to 2°C, which is possible).
Thirdly, a substantial portion of the economic impact (previous modelling exercises indicate around one third) is due not to Australia’s carbon abatement policies but to the actions of other countries. In no sense can that part of it be attributed to the Labor Party’s “carbon bill”. Nor can the Coalition’s weak target change what other countries do.
How to turn a mouse into an elephant
Having chosen the comparison that will provide the loudest headlines in a Murdoch tabloid, Minister Hunt then pulled out his king-sized magnifying glass. How did he get this apparently huge number of $600 billion?
Well, he looked at the real GDP figures (the figures accompanying Chart 3.32) and saw that the difference between the “No carbon price” and the “High price” scenarios in the year 2030 is only $64 billion. Hmmm, not big enough for a scare campaign.
So he added up all of the differences in real GDP over 2013-2030, that is, what you would get by colouring in the gap between the mustard and green lines in the chart. But, hey, real GDP (that is, adjusted to exclude the effects of inflation) is always going to be less impressive than nominal GDP. So he picked an inflation rate of 2.5% (making the basic error of using the CPI instead of the GDP deflator) and, Hey Presto, out pops $633 billion.
Now that’s a headline.
Except it isn’t. At least, it would not be in any newspaper that subjected government claims to a modicum of scrutiny.
$633 billion sounds big, but compared to what? Well, compared to cumulative nominal GDP over 2013-2030, which, using the Minister’s figuring, will amount to $46.1 trillion. So over the whole period the “devastating blow” amounts to a shortfall in nominal GDP of 1.37% in 2030.
But there’s a better way to look at it.
The Treasury modelling shows that, compared with doing nothing, if we join the rest of the world to limit warming to 2°C Australia’s real GDP will be $64 billion dollars lower in 2030. How much is that? Well, under the do-nothing scenario real GDP is projected to grow by almost two thirds between 2013 and 2030. In the last of those years, 2029-2030, it is expected to grow by $69 billion, a little more than the $64 billion decline in GDP due to strong climate policy.
In other words, the “economic devastation” amounts to no more than one year’s delay before Australia’s real GDP expands by two thirds.
Who is mean and tricky?
So here is the question: Are Australians willing to delay the growth in real GDP by 12 months and in doing so play their part in global efforts to tackle climate change, or would they prefer to have the growth a year earlier and do nothing about climate change, sponge off the rest of the world and become an international pariah?
Mr Hunt’s attacks on reasonable efforts to tackle climate change assume that Australians are a mean and nasty people who put tiny increases in future incomes above a safe climate for their children.
I can’t finish without one last comment.
One of the more dishonest deceptions in this saga is the Telegraph’s claim that it has uncovered “the report Shorten didn’t want you to see”. In fact Greg Hunt was the author of this deceit, claiming Labor “would never want these numbers to see the light of day.”
But all of the modelling by Treasury and the Department of Climate Change (now the Department of Environment) was posted on the Authority’s website at the time of the release of its report. The secret “devastating” GDP data from Treasury’s Chart 3.32 were reproduced in its report to the Climate Change Authority plain as day in Table 3.3, and the modelling results were discussed extensively in the Authority’s report.
No Minister, there is no conspiracy between Treasury, your department, the Climate Change Authority and the Labor Party.
Mr Hunt’s confabulations and the Telegraph’s beat-up add to the sorry history of climate scare campaigns. The journalist who accepted uncritically this steaming pile of horse manure from Minister Hunt and spread it thickly over the pages of the Daily Telegraph was the tabloid’s national political editor Simon Benson.
![]()
Clive Hamilton is Professor of Public Ethics, Centre For Applied Philosophy & Public Ethics (CAPPE)
This article was originally published on The Conversation. Read the original article.