A near 100 per cent renewables grid is well within reach, and with little storage

There have been many simulations of a 100% renewable electricity grid for Australia, including some ground-breaking studies from Beyond Zero Emissions, The University of New South Wales and the ANU.

Even the recently released Integrated System Plan from the Australian Energy Market Operator exceeds 97% renewable in the 2040s.

So, what is the point of another one?

Well, this simulation differs from the others in a couple of ways:

It uses actual generation and demand data rather than relying on synthetic traces for those quantities
It is being conducted in near real-time

The benefit of using actual generation and demand data is that some people are sceptical of synthetic wind and solar traces. They may also be dubious when you start modifying demand.

The benefit of the near real-time modelling is that people tend to be more concerned about recent events. If a recent day had very little wind and solar generation, some will take that as proof that you cannot run an electricity grid on renewables. A study based on data from a few years ago is unlikely to change their minds.

Another aspect of near real-time modelling is that it is one thing to optimise a simulation when you have all the data in advance, it is another when you design the simulation before you get the data.

With that in mind, exactly one year ago I started running a simple simulation of Australia’s main electricity grid to show that it can get very close to 100% renewable electricity with approximately five hours of storage (24GW/120GWh).

Each week, I would download demand and generation data from OpenNEM. I left demand unchanged.

The generation data for wind, rooftop and utility solar data was rescaled to supply ~60%, 25% and 20% of demand respectively over the year. For example, over the last year utility solar generation has met 5% of demand. The target for utility solar was 20%, so I rescaled the last 7 days of utility solar data by 4x (ie, 20% divided by 5%).

Note that the sum of 60%, 25% and 20% is greater than 100%. This is important. Any optimised model of a highly renewable grid will have significant amounts of over-generation.

It is better to over-generate and have some curtailment than to generate exactly what you need over the year with significant shortfalls during some months requiring huge amounts of storage or backup. As will be seen later in this article, this simulation ended up having 18% excess generation over the year.

The decision to use 60% wind, 45% solar was based on rough optimisation experiments. A mixture reasonably close to 50:50 takes advantage of the fact that wind and solar are negatively correlated with each other.

Wind tends to generate above average during the night and during winter, complementing the solar generation. I have a bias to wind as it requires less short-term storage, which is used primarily to shift solar generation from the day to the evening and night.

My simulation used the 24GW/120GWh of assumed storage and existing hydro to firm up the wind and solar and match demand.

Both the hydro and storage were assumed highly flexible. Note that I did not use the actual hydro generation data. I completely changed the dispatch of hydro so that it had minimal generation on days when it wasn’t needed, and elevated levels whenever there was a day with significant shortfalls of wind and solar relative to demand.

This is reasonable as most of the hydro capacity on the NEM is associated with large storage dams, making the hydro highly dispatchable. However, to maintain consistency with historical generation, hydro generation was also subject to the following constraints:

Hydro generation was kept between 200 MW and 6,000 MW
Weekly hydro generation was kept above 168 GWh
Annual hydro generation was targeted at between 6% and 9% of demand, though ideally closer to 15,000 GWh, or about 7.5% of demand.

If the wind, solar, storage and hydro was unable to meet demand, then the model supplements generation with ‘Other’. ‘Other’ was deliberately left undefined. It could be gas generation. Indeed, in the short to medium term it is likely to be existing gas peakers that will help firm renewables along with storage and hydro.

But longer term, ‘Other’ could be a highly flexible dispatchable generator running on renewable fuels such as biofuels or green hydrogen, or it could be long-term storage such as Snowy 2.0. When calculating the renewable percentage of the simulation, I have assumed ‘other’ is not renewable, even though it is hoped that in the future ‘other’ will become renewable.

Each week I posted the results of the simulation of the previous seven days to my Twitter account. On Wednesday of this week, I posted the 52nd week, marking a full year of simulations.

I’ve copied the simulation below. It is fitting that the renewable penetration of 99% for the final week of the simulation very closely matched the renewable penetration over the entire 52-week period, 98.8%.

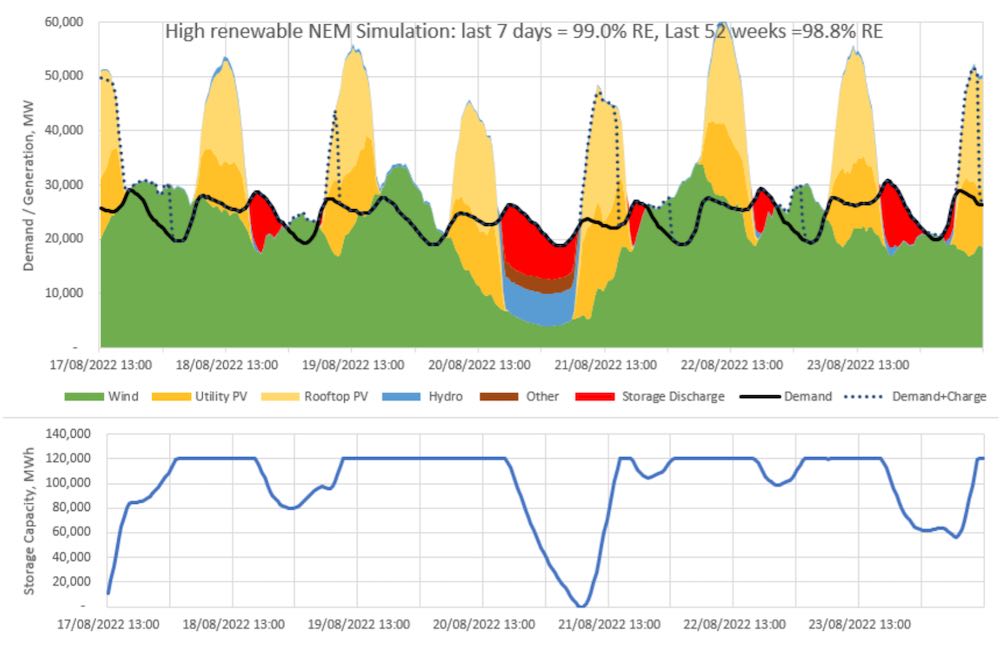
Generation summary

Key results from the 52 weeks of simulations are summarised as follows:

Renewables met 98.8% of demand over the year, with the remaining 1.2% met by ‘Other’
‘Other’ generation peaked at 6.59 GW on the night of July 12. Over the year its average capacity factor was 4.3%.
Hydro met 6.9% of demand. This was lower than my target of 7.5%, and also less than actual hydro generation of 8%. This means that dam storage levels in my simulation would have ended the year higher than they did in the real world.
17% of the wind and solar generation was in excess of requirements and ended up being curtailed.
11% of wind and solar generation went into storage. Storage discharge met 10% of demand.
82% of demand was directly powered by wind and solar without having to pass through storage or be curtailed

The wind and solar generation ended up slightly exceeding the targets of 60%, 20% and 25% for wind, utility solar and rooftop solar respectively.

It is impossible to know in advance if the year would be above or below average, so it is not surprising that they did not exactly hit their target. However, the methodology used to rescale the wind and solar data meant that there was a high probability that they would exceed their targets.

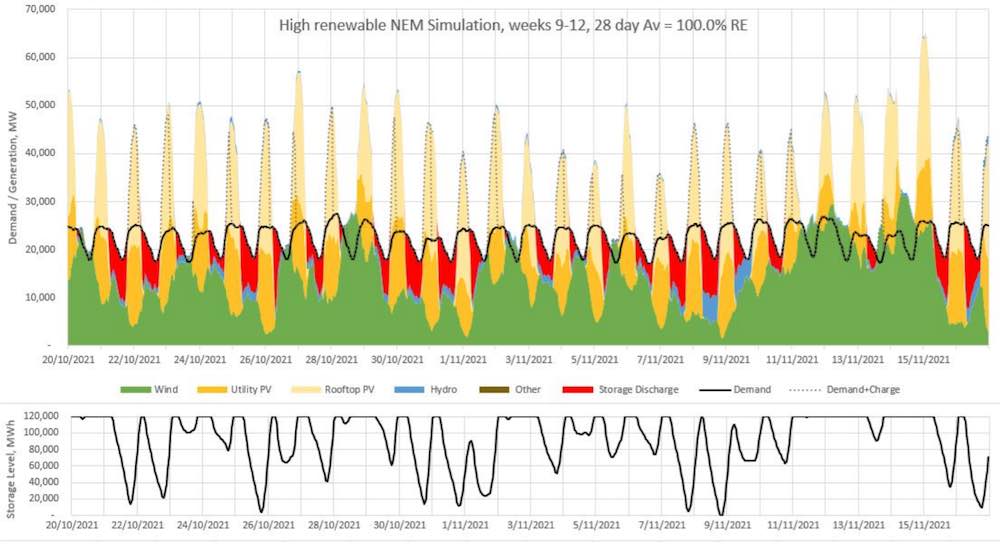
The entire year of simulations in four-week-long blocks has been copied at the end of this article, so you can view all the weeks of simulations as they occurred.

General observations

The graph above shows the weekly fraction of demand that was met by ‘Other’. Levels of ‘Other’ were essentially zero for almost seven months from September to late March. However, by late April, the simulation started to become more ‘interesting’.

Most weeks from late April through to the present required some levels of ‘Other’, due to the inability of wind, solar, storage and hydro to entirely meet demand throughout the week. The week starting on June 29 proved to be the most difficult week of the simulation, with ‘Other’ having to provide 8.1% of demand that week.

The graph illustrates clearly that late autumn and winter will prove to be the most challenging periods for a mostly renewable grid in Australia. Solar generation in late June and early August can often be as low half the annual average.

And while wind tends to be above average during winter, there are often stretches of two or three days in a row that have significantly below average wind. This can leave a significant shortfall in generation that cannot be entirely filled by existing hydro.

The challenge of matching supply and demand during winter will be even more difficult as we start to electrify much more of the gas heating that is present in the southern states, particularly Victoria. Doing so will elevate winter demand much more than summer demand.

It is important to note that wind in Queensland is not well correlated with wind in the southern states. That means that when it is calm in South Australia, Victoria, Tasmania and NSW, it is often windier than average in Queensland. For this reason, it is unfortunate that wind only makes up 3% of Queensland demand, or about one-quarter of the NEM average of 12%.

More wind in QLD will greatly help to improve the geographic diversity of renewable generation, making it easier to match supply and demand over the year. However, it will not completely solve the problem. There will remain many days with poor renewable supply in both the southern states and in Queensland. Increases in Queensland wind generation will make it easier to get closer to 100% renewable electricity, but is unlikely to significantly reduce the peak requirements of ‘Other’.

It is interesting to note that the ISP is predicting that approximately 9GW of peaking gas or liquids will need to be retained in the NEM’s generation mix out to 2050. This is more than the 6.6GW required so far in this study.

However, the ISP is a much more sophisticated model than the simulation I have done here, with increased demand due to increased electrification. It has modelled many years of generation, ensuring that supply stays secure and reliable. It is quite likely that some winters may prove more challenging in a high renewable world than the winter of 2022 simulated here.

Some weeks of particular interest

The first week of interest is week 23, starting on January 26. It was the week of highest demand, peaking at 36GW in the afternoon of Jan 31. Summer is when the NEM normally sees the day with the highest demand. A very small amount of ‘Other’ was required to get through the night of Jan 31, meaning that the week only reached 99.9% renewable.

However, a highly renewable NEM with significant quantities of solar and five hours of storage is well equipped to cope with extreme demand in summer. Extreme demand days typically occur towards the end of a streak of very hot days, which are usually days with very good solar resource.

The very next week starting on February 2 was the week that had the greatest amount of excess generation. Forty three (43) per cent of generation was excess to requirements. You can see that storage spent most of the week at maximum capacity.

Fast forward to week 45, starting June 29, which was the week with the lowest renewable penetration at 91.9%, with ‘Other’ providing the remaining 8.1%. The three-day period from noon on June 29 to noon on July 2 saw ‘Other’ provide 335GWh of energy.

This gives an idea of the requirements of long-term storage that might be required to get through a sustained period of low wind and solar resource without resorting to a gas/biofuel/hydrogen generator.

Zero carbon options for ‘Other’

Zero carbon options for ‘Other’ have previously been mentioned as long-term storage, or peaking generators powered by biofuels or hydrogen. Another option is to increase the amount of over-generation to the extent that ‘Other’ is no longer needed. Some of these are discussed in a little more detail in this section.

Long-term storage

In the previous section it was noted that 335GWh of ‘Other’ was required during a three-day period starting on June 29. A more accurate calculation indicates that 6.6GW/800GWh of long-term storage would have been required to eliminate all ‘Other’ during the 52 weeks of this simulation, assuming a round trip efficiency of 70%.

This storage would have been almost emptied during an 18-day period from June 27 to July 14. For comparison, Snowy 2.0 is 2GW/350GWh of long-term storage, suggesting another 4.6GW/450GWh of long-term storage would be required in the absence of other changes or solutions.

Increase the amount of over-generation

If we built enough wind and solar to meet approximately 170% of demand over the year (ie, 70% over-generation), then supply and demand could have been matched on every day of the year with the help of existing hydro. It could eliminate all instances of ‘Other’ or long-term storage requirements. For comparison, this study had 18% of over-generation. Ideally a use would be found for all this over-generation, such as producing hydrogen or charging EVs, so long as they are able to reduce to near zero on the most difficult days of the year.

Hydrogen fuelled generators

If some of the 18% of generation that was excess to requirements was used to generate hydrogen via 3GW of 70% efficient PEM electrolysers, then it is estimated that they could have run at a utilisation of approximately 66% and produced about 310 million kg of hydrogen over the year. They would have consumed just under half of the excess generation. If this hydrogen was used to fuel a hydrogen reciprocating generator with efficiency of 32%, then they could have generated 3.9TWh of electricity, which is more than enough to cover the 2.5TWh of generation coming from ‘Other’.

Approximately 160 million kg of hydrogen would need to have been stored prior to late April to get through winter. This could either be in underground storage caverns or the hydrogen could be converted to ammonia and stored in above ground tanks.

A combination of all, or some, of the above

Snowy 2.0 is currently being built. So too are hydrogen electrolysers. It is likely that some combination of the three options listed above will all contribute towards zero carbon options for ‘Other’. As such, the above predictions for long-term storage requirements or hydrogen storage should not be taken as gospel. All estimates are highly dependent on assumptions and what other solutions may be used. Moreover, one year of simulations is not nearly enough to accurately determine these quantities.

Costs

The following table and figure indicate the approximate cost of electricity of this simulation, currently $86/MWh. It includes the cost of the wind, solar, hydro and ‘Other’, together with the cost of storage and additional transmission (beyond what is currently installed).

The $/MWh figures show the assumed LCOE of each technology. For storage cost, I’ve assumed all 120GWh of storage is in the form of battery storage, ignoring that the NEM already has approximately 22GWh of pumped hydro storage from Tumut3, Wivenhoe and Shoalhaven.

The battery capex cost was assumed to be $303/kWh, which was obtained from the 2021-22 CSIRO GenCost report, and is the average of the 4-hour and 8-hour battery cost over the 12-year period 2022-2033 in the Global NZE scenario. The battery is assumed to have a 12-year life, so the annual cost is obtained by dividing the total storage cost by 12.

The annual transmission cost is based on AEMO’s 2022 ISP. Its step-change scenario has an average annual spend on REZ augmentation and Flow Path augmentation over the years 2023-2050 of $1.11b to allow 292 TWh/y of additional utility wind and solar. This has been reduced in a pro-rata fashion for the 139 TWh/y of additional utility wind and solar used in this study.

Hydro was priced at a 30% premium to the price received by hydro over the 5-year period 2017-21. ‘Other’ was priced at $600/MWh, based on the estimated LCOE for a peaker gas plant running at 4% CF with fuel cost of $15/GJ.

The final $/MWh figure was obtained by dividing the total annual cost by annual demand. Note that excess generation is included in the annualised cost, but is not included in annual demand. Thus, the model does consider the cost of the 18% of wind and solar generation that was curtailed.

Emissions

The following table shows two estimates of the emission intensity of the simulated grid. The first estimate includes only direct (scope 1) emissions from each technology and arrives at a grid intensity of 9 kg CO2-e per MWh. In this calculation, ‘Other’ is the only technology with direct emissions, assumed to be 700 kg CO2-e / MWh (appropriate for a modern reciprocating engine used as a peaking plant).

The second figure is an estimate of the full lifecycle emissions, including the emissions associated with building each technology. The table assumes the assumed kg CO2-e/MWh for each technology. The figure for the battery is based on assumed embodied emissions of 65 kg/kWh. The resultant estimated full lifecycle emission intensity of the grid is 28 kg CO2-e / MWh.

FAQs

How did I choose the wind and solar scale factors? They are chosen to get wind, utility and rooftop solar close to 60%, 20% and 25% of annual demand, which are my targets for this model. When this study commenced in Aug 2021, the annual penetration rate of wind, utility and rooftop solar on the NEM was 11.1%, 4.0% and 7.3% respectively, so the scale factors were 5.4x, 5.0x and 3.4x respectively. As each week passes and we install more wind and solar, the required scale factors reduce. At week 50, they’d reduced to 5.0x, 4.0x and 2.9x respectively.
How many GW of wind and solar will it take to reach this target penetration? Based on current demand levels as was done in this simulation, it will take approximately 41 GW of wind, 19 GW of utility PV and 39 GW of rooftop PV, based on assumed capacity factors of 34%, 25% and 15% respectively. However, it is likely demand will more than double over the next couple of decades as we electrify sectors such as transport and heating.
Does your model assume perfect foresight? For the first 6 days of each 7-day simulation, my model assumes 24 hours perfect foresight. That is, it knows exactly what the wind, solar and demand will be 24 hours in advance. AEMO can reasonably accurately predict these quantities 24 hours in advance (and beyond), though not perfectly. For the last day of my 7-day simulation, the length of the perfect foresight linearly reduces to zero hours.
Does your simulation consider transmission constraints? No, this simulation is a highly simplified model of the NEM. It assumes generation on any part of the grid can meet demand on any other part of the grid. For this reason, the model is optimistic, and likely under-estimates the amount of curtailment and need for ‘Other’ generation.
Does you simulation change the weightings between states, to reduce the influence of South Australian wind which is currently over-represented, and to increase the weight of QLD wind which is currently under-represented? No, this simulation applies the same scale factors to renewables in each state, which makes the simulation conservative.
What efficiency have I assumed for the storage? 90% 2-way efficiency.